Astrocuriosità | giugno 2021 – La Grande Pera, ovvero il Pianeta Terra
La curiosità del mese a cura di Daniele Spiga

La Grande Pera, ovvero il Pianeta Terra
Tutti ci ricordiamo quando la nostra maestra, nei beati anni della scuola elementare, ci insegnava che “la Terra è schiacciata ai poli, come una mela”. Al che io restavo un po’ perplesso perché, a ben guardare il mio mappamondo, non mi sembrava affatto che assomigliasse a una mela! Certo, nella storia della Fisica le mele sono importanti, basti pensare a quella che (secondo quanto racconta Voltaire) cadde in testa a Newton: ma cosa c’entrano con la forma della Terra?
Se prendete un mappamondo in mano, vi sembrerà una sfera perfetta, e in effetti la nostra amata Terra è molto prossima ad esserlo. Questa cosa è risaputa fin dai tempi di Pitagora e nel pensiero occidentale nessuno l’ha mai messa in dubbio (tranne pochissimi, bizzarri scrittori della tarda antichità, e anche alcuni del XX-XXI secolo, ancora più bizzarri…). Non solo: è dal III secolo a.C. che conosciamo perfino la misura della circonferenza terrestre, grazie al calcolo fatto per la prima volta dal direttore della Biblioteca di Alessandria di Egitto, Eratostene di Cirene, con un metodo ingegnosissimo (vedi nota [1])
Egli calcolò 39375 km. Sapete quanto misura la circonferenza polare della Terra in realtà? 39941 km, solo l’1.4% in più! Applausi a Eratostene.
Senonché, a mano a mano che le misure progredivano in precisione, nel corso degli ultimi secoli, si è iniziato a capire che la Terra non è precisamente una sfera (non mi riferisco al fatto che ci siano montagne, colline, valli ecc.., la cui altezza/profondità è insignificante rispetto alle dimensioni della Terra). E questo, ben prima che si potesse osservare la Terra dallo spazio. Lo strumento che ha permesso di misurare la forma della Terra è davvero semplice: il pendolo.
Il pendolo è un peso fissato a una cordicella di lunghezza fissata, che compie un’oscillazione completa in un tempo che dipende solamente da due cose: 1) la sua lunghezza e 2) l’accelerazione di gravità g. La prima è facile da misurare, mentre il tempo di oscillazione si misura con qualche difficoltà in più perché serve essere molto precisi nella misura (e in effetti, per far le cose per bene servirebbe uno strumento un pochino più complesso, il cosiddetto pendolo reversibile). Ma in ogni caso, misurando tempo e lunghezza, si può risalire a g!
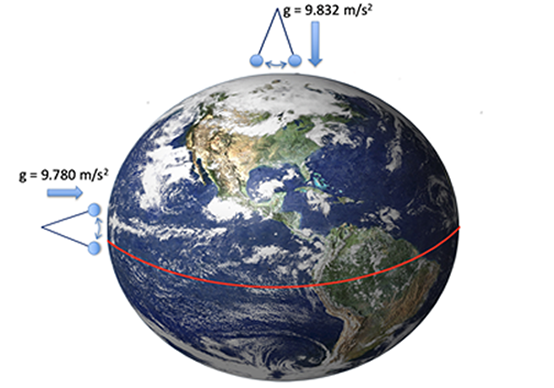
E, visto che la massa della Terra M è conosciuta, si può, in primissima approssimazione, calcolare la distanza dal centro della Terra R con la legge di Newton g = GM/R2 e la costante di gravitazione universale G = 6.67´10-11 m3/kg×s2. Adesso immaginate di prendere l’aereo, anzi, tanti aerei (facendo, presumibilmente, molti tamponi) e di ripetere la misura in giro per il mondo al livello del mare… cosa troverete? Che avvicinandovi ai poli g è maggiore, quindi R è minore! Allora la mia maestra aveva ragione! (vedi nota [2])
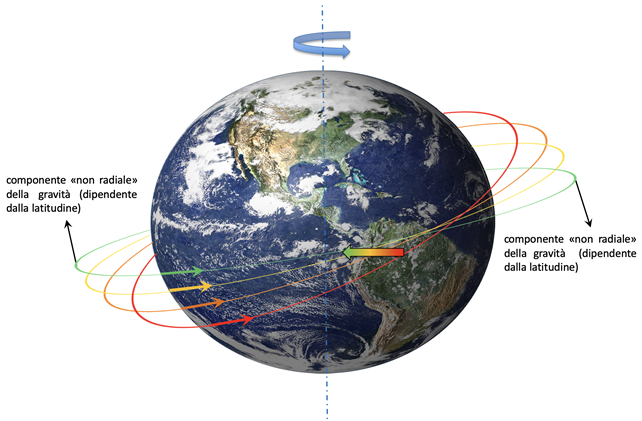
E lo sapete quale è la causa dello schiacciamento polare? La rotazione terrestre! In realtà, questa causa anche un altro effetto, la forza centrifuga, che pure contribuisce a diminuire g andando dai poli all’equatore… ma questa è una storia che racconteremo più avanti.
Oggi sappiamo che la Terra ha un raggio equatoriale di 6378 km e un raggio polare di 6357 km. Una differenza di soli 21 km, che però ha la sua importanza. Tanto per cominciare, domandina: qual è il punto della superficie terrestre più lontano dal suo centro? La cima dell’Everest? Sbagliato, è la vetta del Chimborazo in Ecuador (6310 m), che è sì più basso dell’Everest (8848 m) sul livello del mare, ma è praticamente sull’equatore, dove il livello del mare è più lontano dal centro della Terra. Lo avreste mai detto?
Secondo: lo schiacciamento polare fa sì che la formula che ci dà la gravità terrestre non sia esattamente g = GM/R2, ma sia decisamente più complicata, dipendendo anche dalla latitudine (tecnicamente, si chiama effetto del momento di quadrupolo terrestre). Questo, a sua volta, ha delle conseguenze interessanti sul moto dei satelliti della Terra, le cui orbite non si chiudono mai esattamente ma descrivono una “rosetta”. Se poi l’orbita è inclinata sull’equatore terrestre, il risultato sarà che il piano dell’orbita presenterà il tipico moto di “precessione”, esattamente come una trottola!
E pensate che accadrebbe se i satelliti del GPS non ne tenessero conto.
Ma c’è di peggio. Il fatto che la Terra sia un po’ gonfia all’equatore e, come noto, inclinata sul piano della sua orbita intorno al Sole, fornisce una sorta di leva alla gravità del Sole e della Luna, che cercheranno disperatamente di “raddrizzarla”. Ma la Terra gira e … avete mai provato a raddrizzare un disco mentre gira rapidamente? Non ci riuscirete, ma inizierà a precedere, esattamente come l’orbita del satellite di prima. E così l’asse terrestre, invece di raddrizzarsi, compie un lento movimento descrivendo una specie di cono, che prende appunto il nome di precessione degli equinozi per l’effetto che ha sul calendario (vedi curiosità del mese di gennaio 2021 nota [3]). E manco a dirlo, ciò causa uno spostamento del polo celeste nel corso dei secoli… insomma, questo piccolo schiacciamento della Terra ci movimenta parecchio la vita!
E la mela cosa c’entra? Niente, è un esempio sbagliato. Anche perché il centro di massa della Terra è leggermente spostato nell’emisfero australe e quindi, a rigore, la Terra assomiglia un po’ a una pera, non a una mela! Comunque, una sfera schiacciata ai poli ha un nome preciso in geometria: si chiama sferoide oblato oppure ellissoide di rotazione. Ma se la mia maestra ci avesse detto “la Terra è schiacciata ai poli come uno sferoide oblato, o, se questo termine vi suona oscuro, come un ellissoide di rotazione”, penso che saremmo scappati tutti dalla classe. Decisamente meglio parlare di mele (o di pere).
[1] https://it.wikipedia.org/wiki/Eratostene_di_Cirene#Misura_del_meridiano_terrestre
[2] E ci mancherebbe.